Talks :
- Anderson Hamiltonian
- Laure Dumaz : Anderson localization and the transition towards delocalization
- Abstract : In this talk, we will introduce the Anderson hamiltonian, written as ``- Laplacian + random potential’', and discuss its spectral properties. It is well known that for a wide class of random potentials, localization occurs in one and two dimensions, while a major conjecture is to establish the existence of delocalization in three dimension.
We will focus here on the localization phenomenon in one dimension, in the specific case where the potential is given by the white noise. How does an electron localize in such a random environment? We will see that, as the energy increases, the eigenfunctions exhibit a simple shape, writing as the exponential of a Brownian motion with a drift, a form expected to be universal in one dimension for large energy or small potential limits. Based on joint works with Cyril Labbé. - Immanuel Zachhuber : Energy solutions for multiplicative stochastic NLS on the whole space
- Abstract : I will discuss ongoing work with Antoine Mouzard on the nonlinear Schrödinger equation with multiplicative white noise potential on the whole space. We can prove existence and uniqueness for a natural class of energy solution in dimensions d<=3. This kind of SPDE has been widely studied at this point in the periodic setting but there are few results on R^d and our results on R^3 seem to be the first.
- Random continuum polymers
- Quentin Berger : Stochastic heat equation and directed polymers in dimension d=2
- Abstrast : In this talk, I will review some of the recent results on the Stochastic Heat Equation (SHE) with multiplicative white noise in dimension d=2. The SHE is a stochastic PDE which is ill-defined in its critical dimension d=2 : in that case, very recent results show that a subtle normalisation procedure is needed to make sense of it.
I will present the "probabilistic" approach to this normalisation procedure, which consists in studying the directed polymer model (which can be thought as a discretised SHE) in some critical window of parameters. This is the approach followed by Caravenna, Sun, Zygouras, that allowed them to prove the existence of a (notion of a) solution to the 2D SHE, that they called Critical 2D Stochastic Heat Flow. I will then review some of the properties of this object, highlighting that contributions come from a wide range of ideas, from stochastic analysis to probability and statistical mechanics. - Clément Cosco : The subcritical phase of the two-dimensional stochastic heat equation
- Abstract : In this talk, I will review some recent results concerning the stochastic heat equation (SHE) in the critical dimension d=2. The focus will be on the subcritical phase (small noise limit), where it is now well understood that the equation exhibits a similar behaviour to that of Gaussian log-correlated fields. This is reflected in the extreme value statistics of the solution, which can be compared with those of a (unusual) branching random walk (joint work with Shuta Nakajima and Ofer Zeitouni). I will also present additional results that complement this picture, including a central limit theorem obtained with Anna Donadini and Francesca Cottini in a spatially correlated noise setup.
- Random waves and particles
- Quentin Chauleur : Weakly nonlinear waves: from normal forms to wave turbulence
- Abstract : In this panoramic talk I will be interested in the distribution of energy in Hamiltonian dispersive models with a small nonlinearity, motivated by the theory of wave turbulence and the appearance of Kolmogorov-Zakharov power laws. I will first give some classical results on energy transfer mechanisms in such systems. In the case of random initial conditions, I will then sketch the derivation of the Kinetic Wave Equation in the large box limit.
- Isabelle Gallagher : Derivation of the Boltzmann equation from a gas of hard spheres
- Abstract : The Boltzmann equation is a model describing the density of particles of a dilute gas, in the limit when the number of particles goes to infinity. The derivation of the equation goes back to Lanford in 1975 for short times ; the short time restriction was lifted recently by Deng, Hani and Ma. In this talk will present some ideas of the proofs of those results, as well as the link with fluid equations when the mean free path goes to zero.
- Quantum Field Theory
- Ilya Chevyrev : Observables and renormalisation of stochastic 3D Yang-Mills
- Abstract : In this talk, I will describe a family of observables for 3D quantum Yang-Mills theory based on regularising connections with the YM heat flow. I will describe how these observables can be used to show that there is a unique renormalisation of the stochastic quantisation equation of YM in 3D that preserves gauge symmetries. This complements a recent result on the existence of such renormalisations. Our analysis is based on short time expansions of SPDEs and of regularised Wilson loops, and requires a careful balance between the running time of the dynamic and the regularisation parameter coming from the YM heat flow. Based on joint work with Hao Shen.
- Viet Dang : The Yang–Mills Measure on Surfaces
- Abstract : We report on various works in progress with Bonthonneau–Chhaibi–Rivière–To and Nohra. On a Riemannian surface, we construct a Gibbs measure on the space of distributional connections, the so called "2-dimensional Yang–Mills measure". We rely on some dynamical system to fix the gauge on the space of connections and study transport equations with random driving force.
We show how to recover the formulas for 2D Yang Mills theory as can be found in the works of Witten, Driver, Sengupta and Lévy. In the spirit of the work of Chevyrev, we also discuss how to recover our measure as scaling limit of discrete measures from lattice gauge theories on the surface which is joint work with Nohra. - Dispersive PDEs and randomness
- Nicolas Camps : Gibbs measure for NLS on the 2-sphere
- Abstract : The Gibbs measure problem consists in constructing a unique global invariant flow supported by the measure itself. We address this problem for the cubic nonlinear Schrödinger equation posed on the two-dimensional sphere S2 . In this setting, concentration phenomena along certain geodesics rule out the perturbative approaches that are effective on the torus. To overcome these instabilities, we develop a non-perturbative scheme based on a refined analysis of the probabilistic structure of approximate solutions. Joint work with N. Burq, C. Sun, and N. Tzvetkov.
- Tristan Robert : Regularization by noise for some modulated dispersive PDEs
- Abstract : In this talk, we will consider nonlinear dispersive PDEs where a deterministic noise is added as a distributional time coefficient in front of the dispersion. Despite the roughness of the noise term, we will see that any semilinear dispersive PDE with this noise term is well-posed at least in the same range of regularity as its noiseless counterpart, as soon as well-posedness relies on linear space-time estimates. Building on previous works on this model, we will also observe several regularization by noise phenomena provided that the noise is irregular enough : large data global well-posedness for focusing mass-critical equations, well-posedness at super-critical regularity for strongly non-resonant equations through improved multilinear estimates, and improvement on the Cauchy theory for Kadomtsev-Petviashvili equations through short-time multilinear estimates on longer time scales.
- Stochastic PDEs
- Arnaud Debussche : From correlated to white transport noise in fluid models
- Abstract : Stochastic fluid model with transport noise are popular, the transport noise models unresolved small scales. The main assumption in these models is a very strong separation of scales allowing this representation of small scales by white - ie fully decorrelated - noise. It is therefore natural to investigate whether these models are limits of models with correlated noises. Also, an advantage of correlated noises is that they allow classical calculus. In particular, it allows to revisit the derivation of stochastic models from variational principle and allows to derive equation for the evolution of the noise components. The advantage of having such equations is that in most works, the noise components are considered as given and stationary with respect to time which is non realistic. Coupling stochastic fluid models with these gives a more realistic systems.
- Program :
- Wednesday 12 November
- 10h20 - 10h50 : Welcome coffee
- 10h50 - 11h00 : Presentation of the sessions
- 11h00 - 12h00 : Quentin Berger (Random continuum polymers)
- 12h00 - 13h30 : Lunch
- 13h30 - 14h30 : Ilya Chevryrev (Quantum Field Theory)
- 14h40 - 15h40 : Tristan Robert (Dispersive PDEs and randomness)
- 15h40 - 16h10 : Coffee
- 16h10 - 17h10 : Arnaud Debussche (Stochastic PDEs)
- Thursday 13 November
- 9h30 - 10h30 : Viet Dang (Quantum Field Theory)
- 10h30 - 11h00 : Coffee
- 11h00 - 12h00 : Laure Dumaz (Anderson Hamiltonian)
- 12h00 - 13h30 : Lunch
- 13h30 - 14h30 : Quentin Chauleur (Random waves and particles)
- 14h40 - 15h40 : Nicolas Camps (Dispersive PDEs and randomness)
- 15h40 - 16h10 : Coffee break
- 16h10 - 17h10 : Isabelle Gallagher (Random waves and particles)
- Friday 14 November
- 9h30 - 10h30 : Clément Cosco (Random continuum polymers)
- 10h40 - 11h40 : Immanuel Zachhuber (Anderson Hamiltonian)
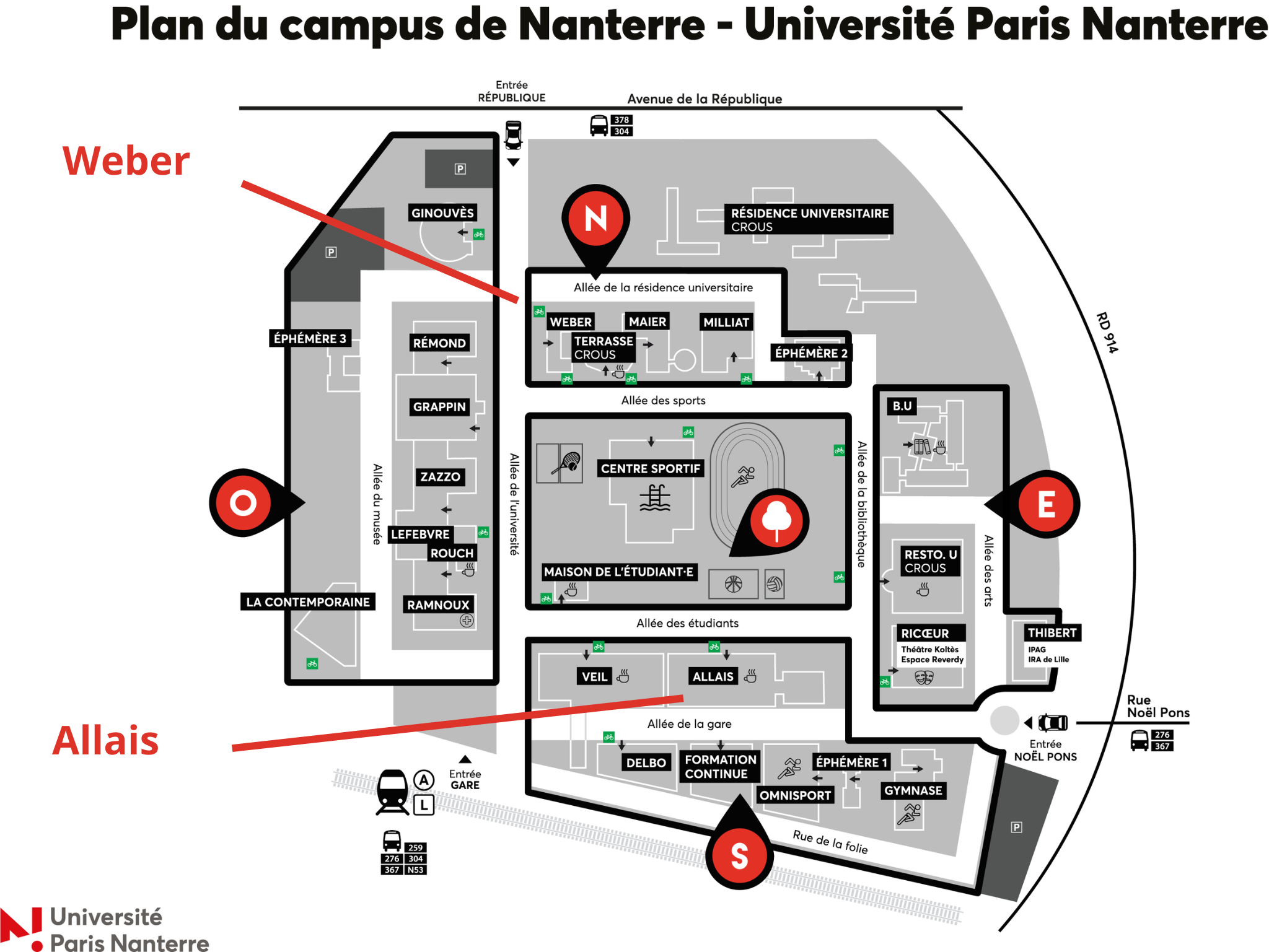
- Venue :
- 12 & 13 November : Weber building (W)
- 14 November : Allais building (G), Amphi F